Анализ и синтез цифровой системы продольного канала автопилота

Тогда матрицы А и В примут вид:

A=. (1.9)

Используя средства МАТLАВ на основе матриц А, В, С, D получим передаточные функции:

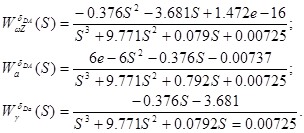(2.0)

Передаточные функции объекта получены ранее с помощью пакета МАТLАВ. Найдем передаточные функции датчиков первичной информации, рулевой машинки, устройств согласования 1 и 2, усилительного блока.

В качестве блока УС1 и УС2 выбираем пропорциональные звенья. При выборе коэффициента для УС1 будем исходить из того, что напряжение питания потенциометрического измерителя МГВ равно ±27 В и максимальное выходное напряжение также равно ±12 В. Входное напряжение вычислителя напряжение - 10 В, поэтому:

Wус1(S)=Кус1=10/13,5=0,74 В/В.

Напряжение питания измерителя типа микросин ДУС равно 36 В, тогда для УС2:

Wус2(S)=Кус2=10/36=0,278 В/В

Для усилителя: Wу(S)=Ку=Uву/Fрв = 10/0.262 = 38. 17 В/рад,

где FРВ - максимальное отклонение руля высоты;

Uву - максимальное выходное напряжение вычислителя.

В качестве передаточной функции сервопривода выберем апериодическое звено с постоянной времени Т=0,1 с:

(2.1)

В качестве датчика угловых скоростей возьмем поплавковый ДУС с передаточной функцией колебательного звена:

аждьаьдапотьвотврв(2.2)

В качестве датчика угла ранее была выбрана малогабаритная гировертикаль, которая является пропорциональным звеном. Считаем измеряемый угол равным ± 12,5°, напряжение питания потенциометрических измерителей равным 27 В, а выходное напряжение равно ± 13,5 В, тогда:

. (2.3)

Под устойчивостью свободного движения ЛА понимается его способность возвращаться в исходное состояние после окончания действия возмущения.

Анализ устойчивости можно произвести по корням характеристического уравнения матрицы состояния А. Так как корни характеристического уравнения совпадают с собственными значениями матрицы А, то используем команду damp(А) в среде МАТLАВ:

-4.02е-003 +2.70е-0021 1.47е-001 2.73е-002

-4.02е-003 -2.70е-0021 1.47е-001 2.73е-002

-9.76е+000 1.ООе+000 9.76е+000

С помощью команды step получим следующие переходные процессы:

Рисунок 1.3- Переходная характеристика системы по ω

-2.5

1500

Рисунок 1.4- Переходная характеристика системы по а

Рисунок1.5-Переходная характеристика системы по γ

Так как все корни характеристического уравнения лежат в левой полуплоскости, то система устойчива, но, исходя из переходных процессов (рис.1.3, 1.4, 1.5) показатели быстродействия не удовлетворяют требованиям ТЗ. Следовательно, необходима коррекция системы.

Параметрический синтез заключается в нахождении коэффициента обратной связи К1 и К2 закона управления, для обеспечения требуемого качества и быстродействия системы управления.

Целью синтеза является определение коэффициентов обратной связи, которые минимизируют некоторые квадратичные критерии качества.

Объект управления и измерительная система описываются зз - моделью. Синтез дискретного регулятора для непрерывной системы будем проводить с помощью команды МАТLАВ - lqrd (Kd,S,L)=lqrd (А, В, Q, R., Тз).